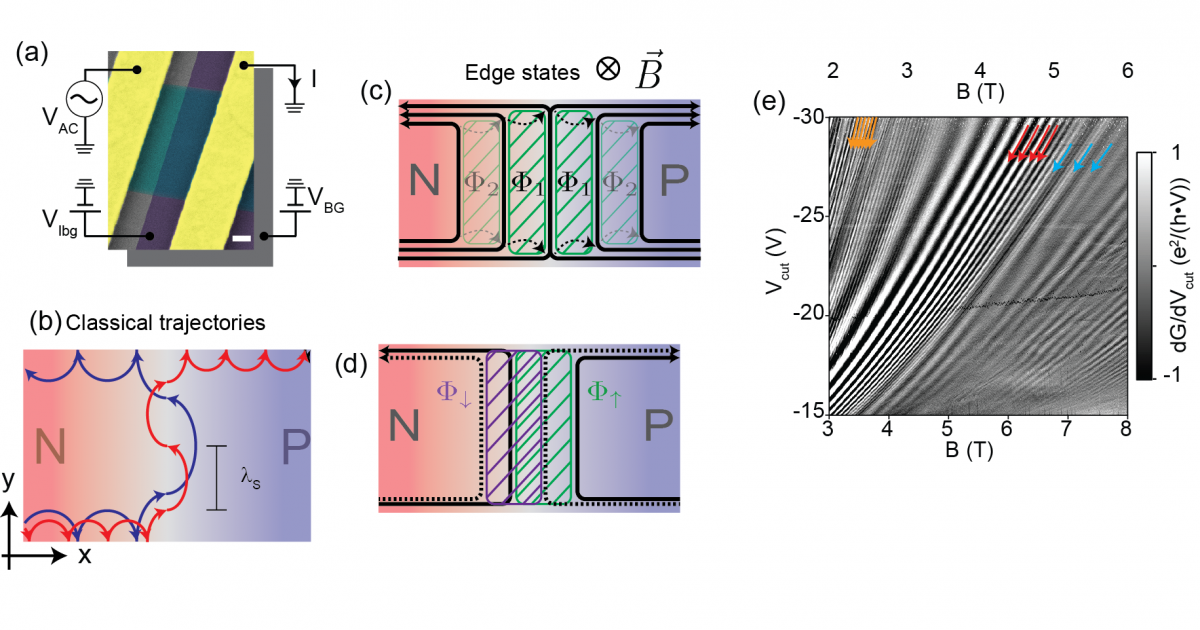
Magneto oscillations in high-mobility graphene pn junctions. a) False coloured SEM image of graphene pn junction. b) Sketch of classical snake states. c)-d) Mach Zender inferometers defined by edge states. e) Measurements on a p-n junction showing a wealth of magneto-oscillation effects.

Clean, suspended graphene samples permit electrons to travel along ballistic trajectories. This means that the mean free path - the average distance an electron travels between collisions (with lattice defects, phonons, or impurities) that change its momentum - is larger than the sample size, which is on the micrometer scale. Different geometries of bottom gates make the realization of inhomogeneous doping along the same graphene flake, like p-n junctions, possible [1]. On one side of a suspended graphene p-n junction current is carried by electrons, while on the other, holes, therefore, the group velocities are opposite. Recent research in collaboration with the Nanoelectronics Group of the University of Basel has shown that by applying a perpendicular magnetic field, the curved ballistic trajectories will snake along this p-n junction since the direction of the Lorentz-force is opposite on the two sides. This effect was observed in the conductance of the sample. [2] We have also investigated large mobility graphene samples encapsulated in hBN. For these samples, not only snake states, but Mach-Zender type interference were observed, originating from the interference of edge channels along the p-n junction [3]. Moreover, for the lowest Landau levels, the conductance also depends on the valley-isospin on the edge [4]. P. Makk and coworkers at the Nanoelectronics group in Basel also demonstrated several other electron-optical elements (wave-guides, beam-splitters, Fabry-Perot resonators, etc.) based on pn junctions [5-8].

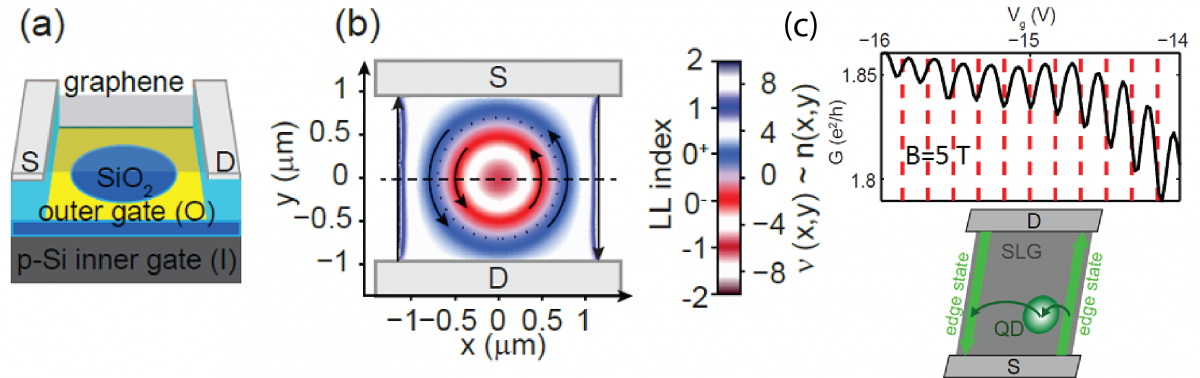(a) Schematic of a double-gated device. (b) Filling factor map of the measured (bilayer graphene) sample based on electrostatic simulations: the circulating quantum Hall channels increase the conductance of quantum Hall plateaus, since they contribute to transport between source (S) and drain (D) contacts. (c) Regular fluctuations were observed in graphene nanoribbons near quantum Hall plateaus due to a single quantum dot causing scattering events between edge states (as drawn in the schematic), or between contacts.

Bulk graphene lacks a band gap, which hinders confinement, however, in a magnetic field, the band structure reforms into a series of Landau levels (LLs). When the Fermi energy is between two LLs, propagating states carry current along the edge, but the bulk of the device is insulating, and an external electrostatic potential can be used to achieve confinement. We have observed, that quantum dots are formed due to localized edge states in potential valleys (or hills, in the case of holes), confined by magnetic fields [9].

We have demonstrated also that the above mechanism can be realized in practice by using artificial electrostatic potentials: for instance, a quantum Hall propagating state have been localized using gate electrodes only [10]. Though charging effects could not be observed due to its macroscopic size, the conductance contribution of this channel, circulating in the bulk of a bilayer graphene sample, have been observed, and its coupling to contacts has been controlled with gate voltages.

References

[1]R. Maurand, P. Rickhaus, P. Makk, S. Hess, E. Tovari, C. Handschin, M. Weiss, and C. Schönenberger, Fabrication of ballistic suspended graphene with local-gating, Carbon  79, 486-492 (2014)

[2] P. Rickhaus, P. Makk, M.-H. Liu, E. Tóvári, M. Weiss, R. Maurand, K. Richter, C. Schönenberger: Snake trajectories in ultraclean graphene p-n junctions, Nature Communications 6, 6470 (2015)

[3] P. Makk, C. Handschin, E. Tóvári, K. Watanabe, T. Taniguchi, K, Richter, M.-H. Liu, and C. Schönenberger, Coexistence of classical snake states and Aharonov-Bohm oscillations along graphene p − n junctions, Phys. Rev. B 98, 035413 (2018)

[4] C. Handschin, P.Makk, P. Rickhaus, R. Maurand, K. Watanabe, T. Taniguchi, K. Richter, Ming-Hao Liu, and C. Schönenberger, Giant Valley-Isospin Conductance Oscillations in Ballistic Graphene, Nano Letters  17, 5389-5393 (2017)

[5] P. Rickhaus, M.-H. Liu, P. Makk, Romain Maurand, S. Hess, S. Zihlmann, M. Weiss, K. Richter, C. Schönenberger, Guiding of Electrons in a Few-Mode Ballistic Graphene Channel, Nano letters 15, 5819 (2015)

[6] C. Handschin, P.Makk, P. Rickhaus, M. -H. Liu, K. Watanabe, T. Taniguchi, K. Richter, and C. Schönenberger, Fabry-Pérot Resonances in a Graphene/hBN Moiré Superlattice, Nano Letters  17, 328-333 (2017)

[7] P. Rickhaus, P. Makk, M. -H. Liu, K. Richter, and C. Schönenberger, Gate tuneable beamsplitter in ballistic graphene, Applied Physics Letters  107, 251901 (2015)

[8] M.-H. Liu, P. Rickhaus, P. Makk, E. Tóvári, R. Maurand, F. Tkatschenko, M. Weiss, C. Schönenberger, K. Richter: Scalable Tight-Binding Model for Graphene, Physical Review Letters 114, 036601 (2015)

[9] E. Tóvári, P. Makk, P. Rickhaus, C. Schönenberger, S. Csonka: Signatures of single quantum dots in graphene nanoribbons within the quantum Hall regime, Nanoscale 8, 11480 (2016)

[10] E. Tóvári, P. Makk, M.-H. Liu, P. Rickhaus, Z. Kovács-Krausz, K. Richter, C. Schönenberger, S. Csonka: Gate-controlled conductance enhancement from quantum Hall channels along graphene p-n junctions, Nanoscale 8, 19910 (2016)